誰もが一度は挑戦したことがある(かもしれない)数独を解くプログラムを作ってみましょう。このプログラムを通じて、アルゴリズムの基本と再帰関数という少し難しそうな概念を楽しく学んでいきます。
- 再帰関数
- バックトラッキングアルゴリズム
- 2次元配列の操作
- 関数の分割と再利用
- 条件分岐とループ
- 問題解決能力
- デバッグスキル
- アルゴリズムの効率
Pythonの学習をより深めたい方へ:「【2024年最新版】Python講座で学べるプログラミングスクール10選を徹底比較」では、Python講座を提供する優秀スクールの比較と選び方をご紹介しています。自分に合ったスクールを見つけたい方は、ぜひチェックしてください。
【Pythonゲーム】数独プログラミングとは?
まずは簡単におさらいしましょう。数独は9×9のグリッドを使ったパズルゲームです。1から9までの数字を使って、以下のルールに従ってグリッドを埋めていきます:
- 各行に1から9までの数字が1つずつ入る
- 各列に1から9までの数字が1つずつ入る
- 3×3の小さなグリッド(全部で9つあります)の中に1から9までの数字が1つずつ入る
以下の図で数独の構造を確認してみましょう。
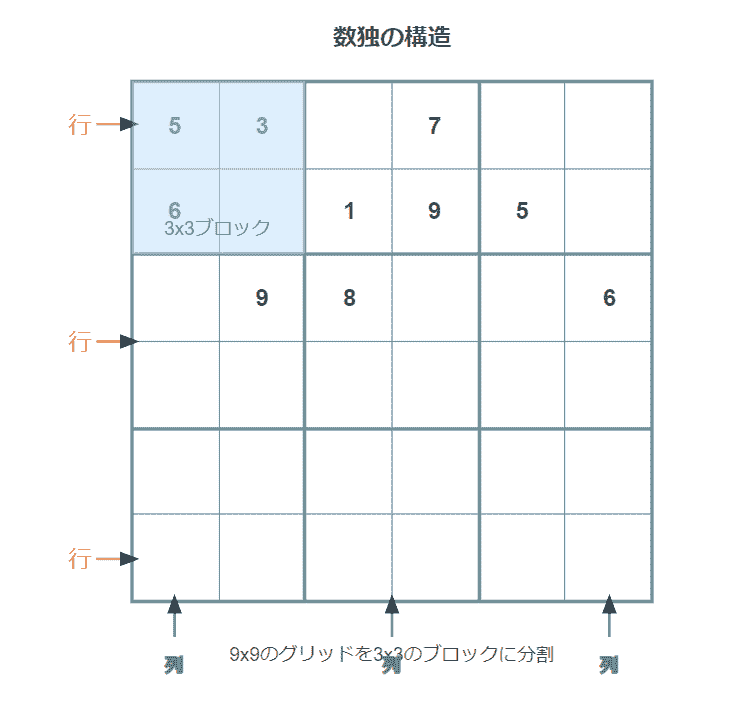
この図では、9×9のグリッドが3×3のブロックに分割されていることがわかります。赤い矢印は行を、青い矢印は列を示しています。黄色で強調された部分は3×3のブロックの例です。これらの行、列、3×3ブロックのそれぞれに1から9までの数字が重複なく入ることが数独のルールです。
数独を解くのは楽しいですが、コンピューターに解かせるとどうなるでしょうか?そこで今回は、Pythonを使って数独を解くプログラムを作ってみます。
【Pythonゲーム】初心者でも簡単!数独プログラミング イメージ画像
コード全体像
def find_empty(board):
for i in range(len(board)):
for j in range(len(board[0])):
if board[i][j] == 0:
return (i, j)
return None
def valid(board, num, pos):
# Check row
for j in range(len(board[0])):
if board[pos[0]][j] == num and pos[1] != j:
return False
# Check column
for i in range(len(board)):
if board[i][pos[1]] == num and pos[0] != i:
return False
# Check box
box_x = pos[1] // 3
box_y = pos[0] // 3
for i in range(box_y*3, box_y*3 + 3):
for j in range(box_x * 3, box_x*3 + 3):
if board[i][j] == num and (i,j) != pos:
return False
return True
def solve(board):
find = find_empty(board)
if not find:
return True
else:
row, col = find
for i in range(1,10):
if valid(board, i, (row, col)):
board[row][col] = i
if solve(board):
return True
board[row][col] = 0
return False
def print_board(board):
for i in range(len(board)):
if i % 3 == 0 and i != 0:
print("- - - - - - - - - - - - - ")
for j in range(len(board[0])):
if j % 3 == 0 and j != 0:
print(" | ", end="")
if j == 8:
print(board[i][j])
else:
print(str(board[i][j]) + " ", end="")
board = [
[5,3,0,0,7,0,0,0,0],
[6,0,0,1,9,5,0,0,0],
[0,9,8,0,0,0,0,6,0],
[8,0,0,0,6,0,0,0,3],
[4,0,0,8,0,3,0,0,1],
[7,0,0,0,2,0,0,0,6],
[0,6,0,0,0,0,2,8,0],
[0,0,0,4,1,9,0,0,5],
[0,0,0,0,8,0,0,7,9]
]
print("元の数独:")
print_board(board)
solve(board)
print("\n解答:")
print_board(board)ゲームの遊び方
このプログラムを使って数独を解くには、以下の手順を踏んでください。
- 上記のコードを作成したPythonファイル(例:sudoku_solver.py)にコピーペーストします。
- board変数に、解きたい数独の初期状態を入力します。空のマスは0で表します。
- プログラムを実行します。
- プログラムが自動的に数独を解き、解答を表示します。
自分で数独を解く場合は、board変数を変更するだけで新しい数独に挑戦できます!

1つひとつ解説していきますので一緒に見ていきましょう
【Pythonゲーム】初心者でも簡単!数独プログラミング コードの解説

では、実際のコードを見ていきましょう。コードは機能ごとに分けて説明します。
- 空のセルを見つける関数
- 数字の妥当性をチェックする関数
- 数独を解く関数(再帰的アプローチ)
- 盤面を表示する関数
- メイン部分:数独を解く
1.空のセルを見つける関数
def find_empty(board):
for i in range(len(board)):
for j in range(len(board[0])):
if board[i][j] == 0:
return (i, j)
return Noneこの関数は、数独の盤面(board)を受け取り、まだ数字が入っていないセル(値が0のセル)を探します。
- boardは9×9の2次元リストで、数独の盤面を表現しています。
- 外側のforループ(i)は行を、内側のforループ(j)は列を走査します。
- board[i][j]で各セルの値にアクセスします。
- 値が0のセル(つまり空のセル)を見つけたら、その位置(行と列の番号)をタプル(i, j)で返します。
- 全てのセルを走査しても空のセルが見つからなかった場合(つまり、盤面が全て埋まっている場合)はNoneを返します。
この関数は、数独を解く過程で次に数字を入れるべき場所を特定するのに使われます。
2.数字の妥当性をチェックする関数
def valid(board, num, pos):
# 行のチェック
for j in range(len(board[0])):
if board[pos[0]][j] == num and pos[1] != j:
return False
# 列のチェック
for i in range(len(board)):
if board[i][pos[1]] == num and pos[0] != i:
return False
# 3x3ボックスのチェック
box_x = pos[1] // 3
box_y = pos[0] // 3
for i in range(box_y*3, box_y*3 + 3):
for j in range(box_x * 3, box_x*3 + 3):
if board[i][j] == num and (i,j) != pos:
return False
return Trueこの関数は、ある位置に特定の数字を入れても問題ないかをチェックします。
- board:数独の盤面(9×9の2次元リスト)
- num:チェックする数字(1から9の整数)
- pos:チェックする位置(行と列の番号のタプル)
関数は以下の3つのチェックを順番に行います。
- 行のチェック:
- pos[0](行番号)を固定し、その行の全ての列(j)をチェックします。
- 同じ行に同じ数字(num)があり、かつそれが現在の位置(pos[1])でない場合、Falseを返します。
- 列のチェック:
- pos[1](列番号)を固定し、その列の全ての行(i)をチェックします。
- 同じ列に同じ数字(num)があり、かつそれが現在の位置(pos[0])でない場合、Falseを返します。
- 3×3ボックスのチェック:
- box_xとbox_yで、チェックする位置が属する3×3ボックスの左上の座標を計算します。
- その3×3ボックス内の全てのセルをチェックします。
- ボックス内に同じ数字(num)があり、かつそれが現在の位置(pos)でない場合、Falseを返します。
全てのチェックをパスすればTrueを返します。これは、その位置にその数字を入れても問題ないということを意味します。
この関数は、数独を解く過程で、ある位置にある数字を入れられるかどうかを判断するのに使われます。
3.数独を解く関数(再帰的アプローチ)
def solve(board):
find = find_empty(board)
if not find:
return True
else:
row, col = find
for i in range(1,10):
if valid(board, i, (row, col)):
board[row][col] = i
if solve(board):
return True
board[row][col] = 0
return Falseこの関数が数独の核心部分です。再帰的なアプローチを使って数独を解きます。
- find_empty(board)を呼び出して、空のセルを探します。
- 空のセルがなければ(not findがTrueなら)、数独は解けたということなのでTrueを返します。
- 空のセルがあれば、その位置(行rowと列col)を取得します。
- 1から9までの数字を順番に試みます(for i in range(1,10):)。
- valid関数を使って、その数字(i)をその位置((row, col))に入れられるかチェックします。
- もし有効な数字であれば:
- その数字をボードに入れます(board[row][col] = i)。
- 再帰的にsolve関数を呼び出します。これが再帰の部分です。
- もしsolveがTrueを返せば(つまり、この選択で数独が解けた)、Trueを返して終了します。
- もしsolveがjFalseを返せば(つまり、この選択では数独が解けなかった)、
その数字を消去(board[row][col] = 0)し、次の数字を試みます。
- 1から9まで全ての数字を試しても解けなかった場合はFalseを返します。
この再帰的なアプローチは、バックトラッキングと呼ばれるアルゴリズムの一例です。可能性のある全ての組み合わせを効率的に試すことができます。
4.盤面を表示する関数
def print_board(board):
for i in range(len(board)):
if i % 3 == 0 and i != 0:
print("- - - - - - - - - - - - - ")
for j in range(len(board[0])):
if j % 3 == 0 and j != 0:
print(" | ", end="")
if j == 8:
print(board[i][j])
else:
print(str(board[i][j]) + " ", end="")この関数は、数独の盤面をコンソールに見やすく表示するためのものです。
- 外側のループ(i)は行を、内側のループ(j)は列を走査します。
- i % 3 == 0 and i != 0の条件で、3行ごとに横線を引きます(最初の行を除く)。
- j % 3 == 0 and j != 0の条件で、3列ごとに縦線を引きます(最初の列を除く)。
- j == 8の条件で、各行の最後の数字を出力した後に改行します。
- それ以外の場合は、数字とスペースを出力し、改行せずに続けます(end=””)。
この表示方法により、3×3のブロックが視覚的に分かりやすくなり、数独の盤面をコンソール上で簡単に確認できます。
5.メイン部分:数独を解く
board = [
[5,3,0,0,7,0,0,0,0],
[6,0,0,1,9,5,0,0,0],
[0,9,8,0,0,0,0,6,0],
[8,0,0,0,6,0,0,0,3],
[4,0,0,8,0,3,0,0,1],
[7,0,0,0,2,0,0,0,6],
[0,6,0,0,0,0,2,8,0],
[0,0,0,4,1,9,0,0,5],
[0,0,0,0,8,0,0,7,9]
]
print("元の数独:")
print_board(board)
solve(board)
print("\n解答:")
print_board(board)ここでは、実際に数独を解いています。
- まず、boardという2次元リストで初期状態の盤面を定義します。0は空のセルを表します。
- print_board(board)を呼び出して、初期状態の盤面を表示します。
- solve(board)を呼び出して、数独を解きます。この関数は直接boardを変更します。
- 再度print_board(board)を呼び出して、解かれた後の盤面(解答)を表示します。
この部分を実行することで、プログラムは自動的に数独を解き、その過程と結果を表示します。

空のセルを見つけ、数字の妥当性をチェックし、数独を解きます。
そして盤面に表示させる流れをつかんで作ってみましょう。
【Pythonゲーム】初心者でも簡単!数独プログラミング このゲームで学べること

このプログラムを通じて、以下のような重要なプログラミングの概念を学ぶことができます。
- 再帰関数: solve関数は自分自身を呼び出す再帰関数です。再帰は複雑な問題を小さな問題に分割して解決するのに役立ちます。数独プログラムでは、各セルを埋める問題を再帰的に解いています。
- バックトラッキングアルゴリズム: このプログラムは、試行錯誤を繰り返しながら解を見つけるバックトラッキングアルゴリズムを使用しています。これは、可能性のある全ての解を効率的に探索する方法です。
- 2次元配列の操作: 数独の盤面は2次元配列(リストのリスト)として表現されており、その操作方法を学べます。インデックスを使って特定のセルにアクセスする方法や、行と列を走査する方法を理解できます。
- 関数の分割と再利用: プログラムを複数の関数(find_empty, valid, solve, print_board)に分割することで、コードの再利用性と可読性が向上します。各関数が特定の役割を持つことで、プログラム全体の構造が明確になります。
- 条件分岐とループ: if文やforループを使って、様々な条件をチェックしたり、繰り返し処理を行ったりする方法を学べます。特に、ネストされたループの使い方(2次元配列の走査など)を理解できます。
- 問題解決能力: 大きな問題(数独を解く)を小さな問題(1つのセルに適切な数字を入れる)に分割して解決する方法を学べます。これは、プログラミングにおける重要な思考法です。
- デバッグスキル: プログラムが期待通りに動作しない場合、各関数の動作を確認しながら問題を特定し、修正する能力が養われます。例えば、print文を追加して中間結果を確認するなどのテクニックを学べます。
- アルゴリズムの効率: バックトラッキングを使うことで、総当たり(ブルートフォース)よりも効率的に解を見つける方法を学べます。これは、計算量の概念を理解する良い例となります。
今回、ゲームを作ってきてさらに難易度設定、Tkinterの使用方法など、ゲームにもっと面白い機能を作ってみたいときはプログラミングスクールで学ぶのもよい選択肢です。こちらの記事ではPythonの講座を集めたスクールを紹介しています「【2024年最新版】Python講座で学べるプログラミングスクール10選を徹底比較」のでPython講座を提供する優秀スクールの比較と選び方の参考にしてください。自分に合ったスクールを見つけたい方は、ぜひチェックしてください。
【Pythonゲーム】初心者でも簡単!数独プログラミングで学ぶアルゴリズム | コピペで気軽にチャレンジ! まとめ

今回は、Pythonを使って数独プログラムを作成しました。このプログラムを通じて、再帰関数やバックトラッキングアルゴリズムなど、プログラミングの重要な概念を学ぶことができます。
- ユーザーが自分で数独の問題を入力できるようにする(例:コンソールから入力を受け付ける)
- グラフィカルユーザーインターフェース(GUI)を追加して、より使いやすくする(例:PyQt5やTkinterを使用)
- 数独を生成する機能を追加する(逆問題を解く)
- アルゴリズムの効率を改善する(例:ヒューリスティックを導入する)
プログラミング初心者の方々にとって、このような実践的なプロジェクトは非常に良い学習機会になります。コードを理解し、自分で修正や拡張を加えてみることで、プログラミングスキルをさらに向上させることができるでしょう。
プログラミングの世界は常に新しいことを学べる環境です。この数独プログラミングをきっかけに、さらに興味深いプロジェクトに挑戦してみてください。理論的な理解と実践的なコーディングを組み合わせることで、より深い洞察力と技術力を身につけることができます。




